Кто решит - тот чоткий! |
  |
 8.8.2013, 20:21 | 8.8.2013, 20:21 |
|
|||
 Арбузик       Карточка |
Проще говоря: задача требует уточнений) ибо наши креативные умы слишком легко ее решают)
вот чего подумала, я не то решила х) при наложении да, Трампо решил. Но раз требовали других решений О.о нате получайте же х) Там их масса. А если без переворотов и бла бла - нерешаема... Да и ладно Я либо ем, либо тортик. |
||
 8.8.2013, 20:55 | 8.8.2013, 20:55 |
|
|||
 Достояние форума           Карточка |
Объясняю популярно. Условие таково - "нужно разрезать имеющуюся фигуру на 2 части, чтоб они совпали при наложении"
в геометрии слово наложение двух частей значит как сказал Хаябуса И всё таки это была задача на конгруэнтность. Вика говорит что Конгруэнтность в геометрии -- "Конгруэнтность (лат. congruens, род. падеж congruentis — «соразмерный», «соответствующий») — отношение эквивалентности на множестве геометрических фигур (отрезков, углов и т. д.). Вводится либо аксиоматически, как например в системе аксиом Гильберта (здесь конгруэнтность, геометрическое равенство применимо, например, к отрезкам, углам или треугольникам, и обозначается инфиксным символом ≅), либо на основе какой-либо группы преобразований, чаще всего движений. Две фигуры называются конгруэнтными, или равными, если существует изометрия плоскости, которая переводит одну в другую. Например, в евклидовой геометрии две фигуры называются конгруэнтными, если одна из них может быть переведена в другую сдвигом, вращением и зеркальным отображением (или их композицией)." Что мы и можем наблюдать в условии как слово "наложение". Это стандартная формулировка подобного рода задач разрезания фигур на части. Я же решил. Нигде не сказано, что нельзя переворачивать, сколько должно быть разрезов, можно ли склеивать и так далее. В условии всё сказано. подчеркну ключевые слова "нужно разрезать имеющуюся фигуру на 2 части, чтоб они совпали при наложении" следует что а) нужно резать б) должно быть ДВЕ части в) они должны совпасть друг с другом г) они должны быть конгруэнтными друг дружке Все необходимые моменты идут из условия! Чтобы прити к этому решению мне понадобилось пол минуты =-= только вот рисую я долго  Вот частая ошибка в решении - наложиваться они должны не одна над другой или под другой, а одна на другую. Если Мы их наложим (всё равно что надстроим как бы) одна над другой - у нас они не будут совпадать - у нас получится прямоугольник (касательно этой задачи) Как бы то ни было - один человек на Хабре подошёл нестандартно к выполнению условий задачи, тем не менее не нарушая самих условий. Он решил задачу посредством пространственной стереометрии! Вот я воспроизвёл то что он там сделал --- 1) режем фигуру вот так  2) свернуть каждую часть острыми углами друг к дружке вот так - получился равноусеченный пустотелый циллиндр - 2 шт. Из двухмерного пространства (мне больше нравится "пространство" чем слово "плоскость" - в данном случае это одно и то же) в трехмерное. он сделал. Условием это не запрещено.  3) налаживаем одна на другую полученые трехмерные фигуры  4) фигуры совпали при наложении. условие соблюдено. задача решена таким вот нестандартным способом. (на фото я специально не совместил их полностью чтоб было видно что там две фигуры а не одна ) 
|
||
 8.8.2013, 20:58 | 8.8.2013, 20:58 |
|
|||
 Арбузик       Карточка |
Профф действительно Профф
Я по геометрии имела 4 из 12 х))) Так что даже пытаться не буду х) Я либо ем, либо тортик. |
||
 8.8.2013, 21:08 | 8.8.2013, 21:08 |
|
|||
 Достояние форума           Карточка |
Профф действительно Профф Я по геометрии имела 4 из 12 х))) Так что даже пытаться не буду х) Это не я решил а какой то умный хмырь )) Вот ещё решение - на Хабре его огласили, но почему то не придали значения. А зря - написавший правильно считал - невежи зазря только облаяли его. Он предложил порезать фигуру повдоль. Просто и легко. Ему сказали - иди отсюда, умник. И не стали слушать и забыли. А ведь он прав - задачу можно решить таким образом. Правда теоретически не представляется возможным, невозможно это сделать просто. Тут кароч тема за "два с половиной пространства". Доказано что евклидово пространство не есть полностью двухмерное! Те линии, которые границы (длина и ширина) имею свою какую-никакую а высоту, она ничтожно мала и близится к абсолютному минимуму, но тем не менее она есть. Таким образом если фигуру порезать повдоль по этому абсолютному минимуму, то получится 2 абсолютно одинаковых фигуры. Условие соблюдено. Решение нестандартное, но с точки зрения геометрии верное. Чисто теоретическое решение. Я кстати позорный двоечник по геометрии - в табели всегда стояло 3, из жалости не оставлять меня на второй год из-за геометрии. Так чта школьную программу я так и не постиг. Доказывать я не умею. В теории - лох. Если завязано только на цифрах - эт пожалуйста, решить можем )) а вот всё остальное звиняйте - только зубриловым и спасался. Щас то я чот более менее понимать стал, но раньше...ну не будем о грустном |
||
 8.8.2013, 21:49 | 8.8.2013, 21:49 |
|
|||
 Арбузик       Карточка |
Это не я решил а какой то умный хмырь )) Вот ещё решение - на Хабре его огласили, но почему то не придали значения. А зря - написавший правильно считал - невежи зазря только облаяли его. Он предложил порезать фигуру повдоль. Просто и легко. Ему сказали - иди отсюда, умник. И не стали слушать и забыли. А ведь он прав - задачу можно решить таким образом. Правда теоретически не представляется возможным, невозможно это сделать просто. Тут кароч тема за "два с половиной пространства". Доказано что евклидово пространство не есть полностью двухмерное! Те линии, которые границы (длина и ширина) имею свою какую-никакую а высоту, она ничтожно мала и близится к абсолютному минимуму, но тем не менее она есть. Таким образом если фигуру порезать повдоль по этому абсолютному минимуму, то получится 2 абсолютно одинаковых фигуры. Условие соблюдено. Решение нестандартное, но с точки зрения геометрии верное. Чисто теоретическое решение. Я кстати позорный двоечник по геометрии - в табели всегда стояло 3, из жалости не оставлять меня на второй год из-за геометрии. Так чта школьную программу я так и не постиг. Доказывать я не умею. В теории - лох. Если завязано только на цифрах - эт пожалуйста, решить можем )) а вот всё остальное звиняйте - только зубриловым и спасался. Щас то я чот более менее понимать стал, но раньше...ну не будем о грустном *пойду положу мозги на тумбочку *,...,* * У меня все пропало из-за болезней, и алгебра с геометрией менялись оценками каждый семестр. Я все могу понять, лишь бы материал излагали нормально или я его не пропускала, а так было: Алгебра: 6 Геометрия: 4 Следующий семестр: Алгебра: 4 Геометрия 6 И так далее два года подряд х))) Я либо ем, либо тортик. |
||
 8.8.2013, 21:54 | 8.8.2013, 21:54 |
|
|||
|
Активный участник    Карточка |
Без коментариев. Не понять мне высших умов...
|
||
 8.8.2013, 22:00 | 8.8.2013, 22:00 |
|
|||
 Ватник и сепаратист       Карточка |
Должен заметить, что в задаче нет ни слова о геометрии, а условие таково, что можно нафантазировать всё что угодно. В следующий раз, ПРОФФ, будь более конкретным. "Неуд" тебе за спешку нас всех позабавить.
|
||
 8.8.2013, 23:39 | 8.8.2013, 23:39 |
|
|||
 Хлоп-хлоп, а не хлюп-хлюп        Карточка |
По мне так, условия задачи вполне конкретные и разночтению не подвергаются.
|
||
 9.8.2013, 0:05 | 9.8.2013, 0:05 |
|
|||
 Житель форума     Карточка |
Доказано что евклидово пространство не есть полностью двухмерное! Те линии, которые границы (длина и ширина) имею свою какую-никакую а высоту, она ничтожно мала и близится к абсолютному минимуму, но тем не менее она есть. Таким образом если фигуру порезать повдоль по этому абсолютному минимуму, то получится 2 абсолютно одинаковых фигуры. Условие соблюдено. Решение нестандартное, но с точки зрения геометрии верное. Чисто теоретическое решение. да, конечно 
 |
||
 9.8.2013, 1:30 | 9.8.2013, 1:30 |
|
|||
 !         Карточка |
Вакатта. Мой даунский вариант сразу летит в ведро
Правда я так и не понял, почему вариант Трампо не подходит. Если можно свернуть детали в трубку, то почему бы просто не перевернуть? Ну... если только дело не в этой самой конгруэнтности, которую я не понял (без наглядных примеров очень трудно теория мне даётся). |
||
 9.8.2013, 1:34 | 9.8.2013, 1:34 |
|
|||
 Арбузик       Карточка |
Вакатта. Мой даунский вариант сразу летит в ведро Правда я так и не понял, почему вариант Трампо не подходит. Если можно свернуть детали в трубку, то почему бы просто не перевернуть? Ну... если только дело не в этой самой конгруэнтности, которую я не понял (без наглядных примеров очень трудно теория мне даётся). Чувак, не бойся, я вообще ничо не понял Я либо ем, либо тортик. |
||
 9.8.2013, 2:01 | 9.8.2013, 2:01 |
|
|||
 !         Карточка |
Чувак, не бойся, я вообще ничо не понял Ну... по идее в таких задачах я хоть сколько-нибудь должен шарить из-за специализации (бывшей (( ), поэтому мне можно (или даже должно) и постыдиться немного) |
||
 9.8.2013, 2:57 | 9.8.2013, 2:57 |
|
|||
 Достояние форума           Карточка |
Должен заметить, что в задаче нет ни слова о геометрии, а условие таково, что можно нафантазировать всё что угодно. В следующий раз, ПРОФФ, будь более конкретным. "Неуд" тебе за спешку нас всех позабавить. НУ как тебе объяснить - условие вполне конкретное, но нафантазировать можно, это да. Ведь только русскоговорящий человек при решении конкретной задачи может уйти бог знает куда. Как нет слова о геометрии????? 1) есть слово "фигура" - термин с геометрии 2) слово "наложение" - применительно к фигуре - из геометрии. 3) собственно сама картинка - тут уж слепой видит что это не физика Конкретики? Это ведь не я придумал - я выдал оригинальную постановку задачи, ничего от себя не добавляя - всё вот оно как было. Я ничо не трогал. Какой ты Трампо, однако, непонятливый - вредный студент |
||
 9.8.2013, 3:17 | 9.8.2013, 3:17 |
|
|||
 Достояние форума           Карточка |
Говоря об увеселении этого мероприятия - мне довольно что хоть как то разбавил скуку Вашу. Просто я хотел посмотреть - а может ещё кто решит как - отлично от моих подходов! Задача в классическом виде "порезали-сложили" нерешабельна, потому приходится делать такого рода хитроумные выкрутасы. То что она не решабельна в классическом виде - это я проверил - так оно и есть, я поизвёл бумагу и наточил заодно ножницы.
Мои способы решений верны теоретически (да и практически только) - но они настолько нестандартные, что Вы меня тут тапками закидаете, как какого таракана за такие решения )) Мне вот подкинули эту задачку и я прямо поизвёлся пока её решал, вроде бы оно мне и нафиг не надо, но я самоуверенно решил поделить на ноль - оно то получилось, но всё же )) Вот я решил эту задачу таким образом - фиг знает что за область геометрии, но тема с плоскостями такая - вот есть пространство (она же плоскость) этой фигуры - да. При резании фигуры на практике (допустим бумагу резаком) мы воздействуем на это пространство другим (плоскость лезвия резака). Получается задействовано теперь 2 отдельных пространства - фигуры и резака. Но тема такая - об отражающих плоскостях. Я не знаю как можно рассказать теорию происходящего - ибо нуб, но практически задачу решить можно таким образом - на плоскость фигуры в любом отрезке сторон фигуры ложиться дополнительная плоскость - отражающая плоскость, от одной части фигуры к другой, дабы разграничить фигуру на 2 части. Смысл того что части фигуры проектируются на отражающую плоскость - создавая своего рода отражение. Таким образом задача будет решена - так как из-за наложения поперк отражающей плоскости - произошло разграничение фигуры на 2 части, части спроецированы на плоскость каждая со своей стороны - идентичность частей достигнута. Только идентичны они каждая своей. |
||
 9.8.2013, 3:35 | 9.8.2013, 3:35 |
|
|||
 !         Карточка |
Вроде понял мысль. Правда она кажется мне слишком читерской по отношению к условию) Впрочем, когда кажется... пойду-ка я лучше спать... да.
|
||
 9.8.2013, 8:36 | 9.8.2013, 8:36 |
|
|||
 Хлоп-хлоп, а не хлюп-хлюп        Карточка |
Правда я так и не понял, почему вариант Трампо не подходит. Если можно свернуть детали в трубку, то почему бы просто не перевернуть? Ну... если только дело не в этой самой конгруэнтности, которую я не понял. Потому что при наложении его половинки не совпадают, верти их не верти. В условии задачи конгруэнтность обозначена. |
||
 9.8.2013, 12:21 | 9.8.2013, 12:21 |
|
|||
 Достояние форума           Карточка |
Вот ещё оригинальный достаточно нашёл вариант. На рождение этого решения у меня ушло мгновение после того как увидел в интернетах гифку одну, там скажем так - изображена скульптура из металлических полосок, выгнутых в слове "любовь", НО камера движется в противоположную часть скульптуры и она неподвижно трансформируется в слово "ненависть" - я фиг знает как назвать это в геометрии, когда одна фигура разная с разных ракурсов. Не уверен точно, но вроде это из геометрии Лобачевского
Ну так вот - 2 ключевых момента в этом нестандартном решении--- 1) Идея такова что фигура эта - "искривлённая плоскость", то есть с одного ракурса может быть одним, с другого другим, с третьего третьим, например есть если посмотреть слева - это круг, посмотреть справа - это треугольник, посмотреть сверху - видимый нами многогранник. 2) Мне думается что самая большая ошибка в решении этой задачи, это то что люди думают что нужно найти решение посредством 1 реза. Вот реализую мысль--- 1) намечаем линии резов  2) режем по линиям, а ту что недорезана до конца отгибаем перепендикулярно фронтальной стороне  3) сравниваем фигуры с ракурса фронтальной стороны - специально не показал полное сравнение, чтоб было видно что я там ничего не отрезал втихушку  Вот. Основная мысль такая - фигура представляет собой "искривлённую плоскость". Движение и ракурс - делают эту фигуру такой которую можно порезать на две части и провести конгруэнтность исходя лишь с одного ракурса. При движении на другой ракурс, то есть в противоположную сторону, можно увидеть что эта верхушка одной части, которая надрезана - она визуально сохраняется, в отличие от первичного ракурса, где мы визуально не наблюдаем эту верхушку, потому что она поставлена боком, но никуда не исчезла, просто мы её не видим. |
||
 9.8.2013, 12:27 | 9.8.2013, 12:27 |
|
|||
 Достояние форума           Карточка |
На этом - я иссяк как генератор идей решения. Как ещё решить можно - фиг его знает, но раз нашлись такие "способы решения", то разумно предположить, что возможны ещё
не покидаете ещё вариантов решения? |
||
 9.8.2013, 17:47 | 9.8.2013, 17:47 |
|
|||
     Карточка |
Если можно свернуть детали в трубку, то почему бы просто не перевернуть? "В евклидовой геометрии две фигуры называются конгруэнтными, если одна из них может быть переведена в другую сдвигом, вращением и зеркальным отображением (или их композицией)." Самое главное, чтобы фигуры после этих манипуляций вышли одинаковыми.  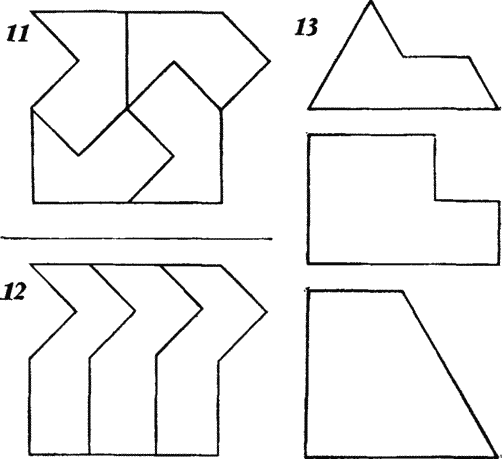
|
||
 9.8.2013, 18:00 | 9.8.2013, 18:00 |
|
|||
 !         Карточка |
"В евклидовой геометрии две фигуры называются конгруэнтными, если одна из них может быть переведена в другую сдвигом, вращением и зеркальным отображением (или их композицией)." Самое главное, чтобы фигуры после этих манипуляций вышли одинаковыми. Спасибо)) Вроде въехал. |
||
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0
| Текстовая версия | Сейчас: 4.2.2026, 12:17 |

























